在零维系统中,系统被简化为集中参数的物理量集合,便于理论上的分析与求解。本篇从零维系统的热自燃工况出发,对不同因素——主要地是系统初温 $T_0$ 与器壁散热系数 $\eta$ ——于热工况的影响进行研究,以确定零维系统燃烧过程中需要注意控制的因素。
理论分析
在布满均匀混合气(包含反应物)的零维系统中,可以简单列出其热平衡方程:
\[Q_v = Q_1 - Q_2\]其中:
- $Q_v = V\rho c_v\frac{\mathrm{d}T}{\mathrm{d}\tau}$ 为系统内混合气体吸收的热量;
- $Q_1 = k_0\exp(-\frac{E}{RT})C^nVQ$ 为系统中发生燃烧反应所产生的热量;
- $Q_2 = \eta S(T-T_w)$ 为系统通过器壁散发的热量。
注意到以上三项热量表达式中,除去 $T$(系统温度)以外的其他量均可视为常量,因此从以上等式中可以反解出一个关于 $T$ 的微分方程:
\[\frac{\mathrm{d}T}{\mathrm{d}\tau}=\frac1{V\rho c_v}\left[k_0\exp\left(-\frac{E}{RT}\right)C^nVQ - \eta S(T-T_0)\right]\]另有初值条件 $T(0)=T_0$ 利用简单的数值解法,即可以很快求解出该方程的数值解,进而得到 $T=T(t)$ 的变化规律。
模型实现
函数封装
由于接下来要研究 $T_0$ 与 $\eta$ 取不同值时温度的变化,故最好先将方程的求解模型封装为一个可方便调用的函数,以便之后直接使用。
首先,引用必要的库——主要是数学运算与作图:
import matplotlib.pyplot as plt
from math import *
接下来,将各个参数的值输入到程序中($T$ 与 $\eta$ 将作为待定变量,安排在函数的参数列表中):
k0 = 100.0 # 频率因子
E = 1e5 # 活化能
R = 8.314 # 气体常数
C = 1.0 # 反应物浓度
n = 1.0 # 反应级数
V = 1.0 # 容器体积
Q = 2e7 # 燃烧热
Tw = 800.0 # 器壁温度
S = 6.0 # 散热面积
rho = 1.0 # 混合物密度
cv = 1e3 # 混合物比热
万事俱备,只欠函数。接下来定义可调用的函数:
Q1 = lambda y: k0 * exp(-E / y / R) * C ** n * V * Q # 反应热量
Q2 = lambda y, eta: eta * S * (y - Tw) # 散热量
def getTemperature(T0=800.0, eta=5.0, dt=.1, N=10000):
'''
利用一阶预估-校正公式求解零维系统热工况.
Args:
T0: 系统初温.
eta: 系统器壁散热系数.
dt: 求解的时间步长.
N: 迭代次数.
'''
t = [0] # 时间节点
T = [T0] # 温度节点
f = lambda y: (Q1(y) - Q2(y, eta)) / (V * rho * cv) # 温度导数表达式
for i in range(N):
t.append(t[-1] + dt)
T_i = T[-1]
p_i = T_i + f(T_i) * dt
T_j = T_i + f(p_i) * dt
T.append(T_j)
return t, T # 返回时间节点与温度节点
以上的默认值是按第一小问的要求定义的,现在即可尝试一下求解的结果(绘图展示):
t, T = getTemperature()
plt.plot(t, T)
plt.xlabel(r'$t$')
plt.ylabel(r'$T$')
plt.title(r'Temperature vs. time, $T_0=800.0$, $\eta=5.0$')
plt.show()
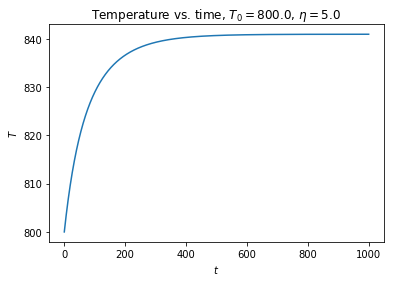
图中的变化规律表明:系统的温度起初上升很快,当达到 $840$ 附近时便趋于稳定。这说明:系统在此情形下,虽然温度逐渐升高但未能发生自然,最终趋于一个稳定熄火点。
系统初温对热工况的影响
以下来研究系统初温 $T_0$ 取不同值时系统热工况的变化状况。这里取 $T_0$ 从 $300$ 到 $1100$ 的各个值:
T0_list = range(300, 1100 + 1, 100)
for T0_i in T0_list:
t, T = getTemperature(T0=T0_i, N=1800)
plt.plot(t, T)
plt.xlabel(r'$t$')
plt.ylabel(r'$T$')
plt.ylim([300, 1300])
plt.legend([r'$T_0=' + str(T0_i) + r'$' for T0_i in T0_list])
plt.title(r'Temperature vs. time, $\eta=5.0$')
plt.show()
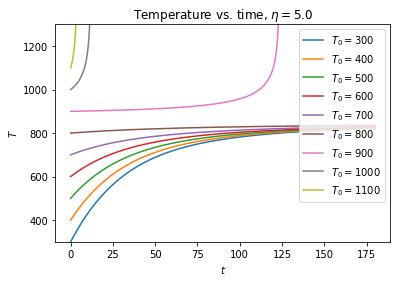
从以上一个序列的曲线可以看出:
- 对于 $T_0 \leq T_w$ 的情形,系统的温度快速趋向于一个略高于 $800$ 的温度——从之前的例子可以看出,这个温度点应该在 $840$ 左右。
- 对于 $T_0 > T_w$ 的情形,系统的上升得更快,并从某一个点开始急剧升高,似乎没有终止的渐进温度。事实上,若将时间长度再取大些,以上的 $T_0=1000$ 或 $T_0=1100$ 之情形将计算出 $10^7$ 以上的温度值,这显然不合实际,但也说明:在反应按初始状态持续进行的情况下系统温度将持续升高。
为找到两种形态之间的转折「临界点」,进一步将温度取值范围锁定在 $800$ 至 $900$ 之间,以 $10$ 为步长进行探索:
T0_list = range(800, 900 + 1, 10)
for T0_i in T0_list:
t, T = getTemperature(T0=T0_i, N=6000)
plt.plot(t, T)
plt.xlabel(r'$t$')
plt.ylabel(r'$T$')
plt.ylim([800, 1000])
plt.legend([r'$T_0=' + str(T0_i) + r'$' for T0_i in T0_list])
plt.title(r'Temperature vs. time, $\eta=5.0$')
plt.show()
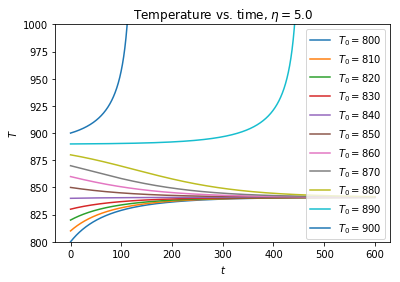
可观察到:当系统初温 $T_0$ 不达到 890 时,无论其温度是低于还是高于 840,其都将趋于这个稳定值(即熄火);而当系统温度高于 890 之后,系统温度便可以持续升高。因此可以断定:系统只有在初温达 890 以上时,才能够正常燃烧,否则将会熄火。
与老师所给的参考结果对照,这里求出的结果似乎有些怪异。为了验证结果的有效性,利用上面已定义的 $Q_1$ 与 $Q_2$ 表达式绘制出热工况曲线:
T = range(800, 1000, 5)
Q_1 = [Q1(T_i) for T_i in T]
Q_2 = [Q2(T_i, 5.0) for T_i in T]
plt.plot(T, Q_1)
plt.plot(T, Q_2)
plt.xlabel(r'$T$')
plt.ylabel(r'$Q$')
plt.legend([r'$Q_1$(react. heat)', r'$Q_2$(heat dissp.)'])
plt.title(r'0-element sys. thermal conditon, $\eta=5.0$')
plt.show()
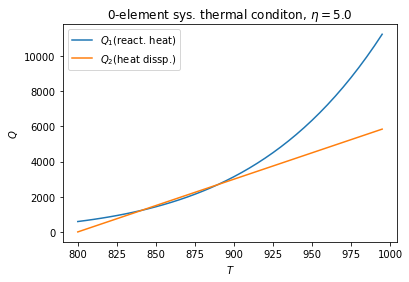
从此图可以看出,这个系统实际上处于课本中所提的第二种情况——不稳定工况。系统在 840 – 890 的温度区段间,散热高于反应热,系统无法点燃。840 为该情形下的一个熄火点,而 890 则是一个点燃点。只有当系统初温达到 890 以上时,系统才能够正常燃烧,这与上面所得的结论一致。
系统散热系数对热工况的影响
现在,固定系统初温 $T_0=800$,转而探究散热系数 $\eta$ 对系统热工况的影响。仍采用已封装好的函数,一次性绘制出 $\eta$ 从 1 变动到 10 之情况下的热工况变化;这里,参考课堂展示的绘图结果,取定值点 1, 2, 3, 4, 4.2, 4.4, 4.6, 4.8, 5, 6, 7, 8, 9, 10.
eta_list = [1, 2, 3, 4, 4.2, 4.4, 4.6, 4.8, 5, 6, 7, 8, 9, 10]
for eta_i in eta_list:
t, T = getTemperature(eta=eta_i, N=20000)
plt.plot(t, T)
plt.xlabel(r'$t$')
plt.ylabel(r'$T$')
plt.ylim([800, 1200])
lg = plt.legend([r'$\eta=' + str(eta_i) + r'$' for eta_i in eta_list], fontsize='x-small')
plt.title(r'Temperature vs. time, $T_0=800.0$')
plt.show()

可以看出,$\eta$ 的临界点大约出现在 4.6 – 4.8 之间。若 $\eta$ 的取值在临界点以上,则在给定系统初温的情况下系统将趋于熄灭;否则,系统将能够点燃,正常燃烧。为观察此范围内的热工况变化情况看,进一步绘出热工况图:
T = range(845, 860)
Q_1 = [Q1(T_i) for T_i in T]
eta_list = [4.6, 4.7, 4.8]
plt.plot(T, Q_1)
for eta_i in eta_list:
Q_2 = [Q2(T_i, eta_i) for T_i in T]
plt.plot(T, Q_2, '--', linewidth=1)
plt.xlabel(r'$T$')
plt.ylabel(r'$Q$')
lg_list = [r'$Q_1$(react. heat)']
lg_list += [r'$Q_2$(heat dissp., $\eta=' + str(eta_i) + '$)' for eta_i in eta_list]
plt.legend(lg_list)
plt.title(r'0-element sys. thermal conditon under different $\eta$')
plt.show()

可以看出,当 $\eta$ 从 4.8 逐渐降低至 4.6 时,终于与产热曲线产生交点,进而从熄火工况过渡到稳定工况。可见,在系统初温难以改变的情况下,改变系统的散热工况有望使原本处于熄火工况的系统正常燃烧。
考虑浓度变化的模型修正
在以上的模拟过程中,并未考虑燃料与氧气的浓度将在反应过程中逐步下降,因此才会在系统初温较高时发生温度无止境上升的不合理情况。为此,进一步引入燃料 $F$ 与氧气 $O_2$ 两个量,将它们的变化纳入模型之中;为此,需要对原来的 getTemperature 函数做一定的修改。
假定燃烧反应按方程式 $F + O_2 = FO_2$ 进行,并进一步假设这是一个基元反应(或言,此反应符合质量作用定律),则可以按质量作用定律及 Arrhenius 定律写出燃料与氧气的浓度微分方程:
\[\begin{cases} \dfrac{\mathrm{d}C_F}{\mathrm{d}\tau} = k_0\exp\left(-\dfrac{E}{RT}\right)C_FC_{O_2}\\[5pt] \dfrac{\mathrm{d}C_{O_2}}{\mathrm{d}\tau} = k_0\exp\left(-\dfrac{E}{RT}\right)C_FC_{O_2} \end{cases}\]两种气体的消耗率相同,可以用同一个函数计算出来。同时,在此模型下,系统的热平衡模型也应修正为:
\[\frac{\mathrm{d}T}{\mathrm{d}\tau}=\frac1{V\rho c_v}\left[k_0\exp\left(-\frac{E}{RT}\right)C_FC_{O_2}VQ - \eta S(T-T_0)\right]\]posOnly = lambda x: x if x > 0 else 0 # 截断函数,防止浓度小于 0
dc = lambda y, cf, co2: k0 * exp(-E / R / y) * posOnly(cf) * posOnly(co2) # 浓度变化(使用使应将其作为减数)
Q1 = lambda y, cf, co2: dc(y, cf, co2) * V * Q # 反应热量
Q2 = lambda y, eta: eta * S * (y - Tw) # 散热量
def getTemperature(T0=800.0, eta=5.0, dt=.01, N=100000, CF_0 = 1.0, CO2_0 = 1.0):
'''
利用一阶预估-校正公式求解零维系统热工况,考虑浓度变化的影响.
Args:
T0: 系统初温.
eta: 系统器壁散热系数.
dt: 求解的时间步长.
N: 迭代次数.
'''
t = [0] # 时间节点
T = [T0] # 温度节点
CF = [CF_0] # 燃料浓度节点
CO2 = [CO2_0] # 氧气浓度节点
f = lambda y, cf, co2: (Q1(y, cf, co2) - Q2(y, eta)) / (V * rho * cv) # 温度导数表达式
for i in range(N):
t.append(t[-1] + dt)
T_i, CF_i, CO2_i = T[-1], CF[-1], CO2[-1]
p_i = T_i + f(T_i, CF_i, CO2_i) * dt
dc_i = dc(p_i, CF_i, CO2_i)
CF_j, CO2_j = CF_i - dc_i * dt, CO2_i - dc_i * dt
T_j = T_i + f(p_i, CF_j, CO2_j) * dt
T.append(T_j)
return t, T, CF, CO2 # 返回各参量节点列表
以上函数定义中的默认参数值即为第一小问给定的条件。直接利用其得出此条件下的温度变化规律:
t, T, _, _ = getTemperature()
plt.plot(t, T)
plt.xlabel(r'$t$')
plt.ylabel(r'$T$')
plt.title(r'Temperature vs. time, $T_0=800.0$, $\eta=5.0$')
plt.show()

这个结果看起来与上面未修正的模型差不多,可能的原因是:在此条件下系统没有点燃,燃料与氧气因此消耗很慢,没有体现在结果之中。
混合比的影响
以下来利用上面所得的修正模型探究燃料/氧气混合比的影响。这里设定浓度比为以下几种,其中设定氧气与燃料的浓度之和恒为 2.0:
- $C_{F0}=0.1$, $C_{O_20}=1.9$;
- $C_{F0}=0.5$, $C_{O_20}=1.5$;
- $C_{F0}=0.6$, $C_{O_20}=1.4$;
- $C_{F0}=0.75$, $C_{O_20}=1.25$;
- $C_{F0}=0.8$, $C_{O_20}=1.2$;
- $C_{F0}=0.9$, $C_{O_20}=1.1$;
- $C_{F0}=C_{O_20}=1$;
考虑到燃料与氧气在反应中居于对称地位,故不再重复讨论氧气与燃料浓度对换的情形。
CF_list = np.array([.1, .5, .6, .75, .8, .9, 1.])
CO2_list = 2 - CF_list
for CF_i, CO2_i in zip(CF_list, CO2_list):
t, T, _, _ = getTemperature(T0=900, CF_0=CF_i, CO2_0=CO2_i)
plt.plot(t, T)
plt.xlabel(r'$t$')
plt.ylabel(r'$T$')
plt.ylim([800, 1000])
plt.legend([r'$C_F(0)=' + str(CF_i) + r'$, $C_{O_2}(0)=' + str(CO2_i) + r'$' for CF_i, CO2_i in zip(CF_list, CO2_list)])
plt.title(r'Temperature vs. time, $T_0=900.0$')
plt.show()

从上图中可以观察到:随着燃料的配比从一对一趋于失衡,温升也逐渐变缓。配比的临界点出现在 $C_{F0}$ 为 0.75 – 0.8(即空气过量系数 $\alpha$ 介于 $\frac53$ 与 $\frac32$)之间的某一点,此时系统由正常燃烧工况急转为熄火工况;且配比越失衡,系统最终的温度越低(易见当两种成分之一为 0 时,系统的温度将保持为壁温 800 度)。
以上这种现象是容易解释的:随着配比的失衡,两种反应物中的一方有多余成分无法参与到反应之中释放反应热,反而成为吸热的累赘。配比失衡达到一定程度时,反应热不足以满足系统散热与多余成分吸热的需要,系统也便无法由燃烧积聚热量,因此便由正常燃烧工况转为熄火工况。
爆炸极限的绘制
利用以上已修正的模型,可以在不同的成分配比、不同的系统初温下绘制出着火区的界限,此图即是生产中非常重要的「爆炸极限」示意图。在这个工作中,系统温度 $T$ 随时间 $t$ 变化的具体规律已不重要,重要的是判断出系统是否处于着火工况内;这一点,可以利用上面已定义的 $Q_1$、$Q_2$ 值来判断:
- 若初始时间点上 $Q_1>Q_2$,表明初始时反应热即高于散热,此时系统处于着火工况内;
- 否则,表明初始时的反应热小于散热,系统温度将逐渐下降,此时系统处于熄火工况内。
然而,仅利用初始的热量状态来判断,并不足够可靠;例如,在系统初温为 800、散热系数为 $\eta=5.0$ 时,系统温度虽然会持续上升至 840 左右,但终归不是着火工况。为了进一步排除这种状态,应注意到:与这种熄灭工况下的温升相较,燃烧工况下的温升是越来越快的,即在一段时间后 $Q_1-Q_2$ 的值将比初始状态下更高(更大的热量为系统所吸收)。因此,可以进一步提出第三条判据:
- 在确定的某一时间点,检查 $Q_1 - Q_2$ 的值(可以为负);若该值较初始时更高,则说明系统的确处于着火工况内。
下面就依照着这三条判据,对燃料质量分数 $x$ 从 $0$ 到 $1$ 的范围进行判断,确定爆炸极限的「示意图」。始终设定系统的散热系数 $\eta=5.0$(函数默认值),而设定第三条判据中的确定时间点为 $t=1$。
x = np.linspace(0, 1, 50 + 1) # 质量分数分布
CF_list = 2. * x
CO2_list = 2 - CF_list
eta_list = list(range(1, 7))
for eta_i in eta_list:
Tf = [] # 着火温度点
for CF_i, CO2_i in zip(CF_list, CO2_list):
for T in np.linspace(600, 1500, 10000):
if Q1(T, CF_i, CO2_i) > Q2(T, eta_i):
_, T_10, CF_10, CO2_10 = getTemperature(T0=T, CF_0=CF_i, CO2_0=CO2_i, dt=.01, N=100, eta=eta_i)
T_10, CF_10, CO2_10 = T_10[-1], CF_10[-1], CO2_10[-1]
if Q1(T_10, CF_10, CO2_10) - Q2(T_10, eta_i) > Q1(T, CF_i, CO2_i) - Q2(T, eta_i):
Tf.append(T)
break
plt.plot(x[1:-1], Tf)
plt.title('Explosive limit under different $\eta$')
plt.xlabel(r'$x$')
plt.ylabel(r'$T_0$')
lg = plt.legend([r'$\eta=' + str(eta) + r'$' for eta in eta_list])
plt.show()

这里,图线呈现出「两边高,中间低」的 U 型,与我们的预期一致。容易看出:随着系统散热条件的改善,曲线逐渐上移,在某一给定温度下的爆炸极限(相当于作一条线水平线与 U 型曲线的交点距)也随之收窄。部分曲线中存在不太正常的尖点,可能是由于数值解法中的步长偏大,造成了误差。